Menyelesaikan Persamaan Kuadrat dengan Rumus Kuadrat
Pada pembahasan ini kita akan menentukan suatu rumus yang dapat digunakan untuk menentukan selesaian dari persamaan kuadrat ax2 + bx + c = 0. Sebelum itu, kita akan mencoba untuk menyelesaikan persamaan kuadrat 2x2 + 5x + 3 = 0. Perhatikan langkah-langkah dalam menyelesaikan 2x2 + 5x + 3 = 0 dengan melengkapkan kuadrat berikut.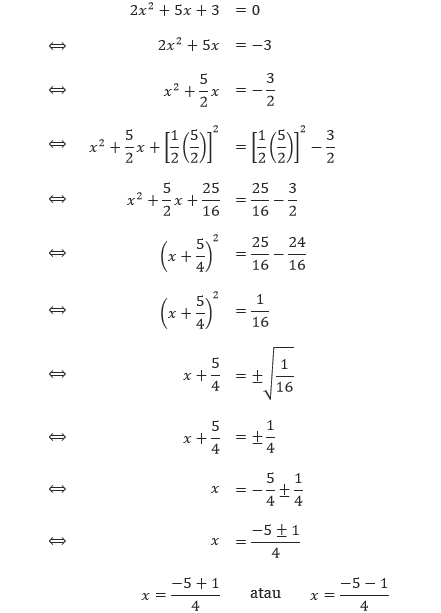
Sehingga diperoleh selesaian-selesaian dari persamaan kuadrat di atas adalah x = –1 dan x = –3/2. Berdasarkan langkah-langkah di atas, kita akan menentukan suatu rumus yang dapat digunakan untuk menyelesaikan persamaan kuadrat ax2 + bx + c = 0.

Solusi-solusi dari persamaan kuadrat ax2 + bx + c = 0 di atas selanjutnya disebut sebagai rumus kuadrat, yang dapat digunakan untuk menyelesaikan semua persamaan kuadrat.
Rumus KuadratCatatan Perlu diketahui bahwa nilai a, b, dan c diperoleh dari persamaan kuadrat yang ditulis ke dalam bentuk standar. Untuk 3x2 – 5x = –7, a = 3, b = –5, tetapi c ≠ –7! Bentuk standar dari persamaan tersebut adalah 3x2 – 5x + 7 = 0, sehingga nilai c dari persamaan tersebut adalah 7.
Jika ax2 + bx + c = 0, dengan a, b, c bilangan real dan a ≠ 0, maka
atau dapat dituliskan menjadi,
Contoh 1: Menyelesaikan Persamaan Kuadrat dengan Rumus Kuadrat
Selesaikan persamaan 4x2 + 1 = 8x dengan menggunakan rumus kuadrat. Nyatakan solusi-solusinya dalam bentuk eksak dan bentuk desimalnya (tiga angka di belakang koma). Ujilah salah satu selesaian eksaknya ke dalam persamaan.
Pembahasan Persamaan kuadrat 4x2 + 1 = 8x memiliki bentuk standar 4x2 – 8x + 1 = 0. Sehingga dari bentuk standar tersebut kita peroleh a = 4, b = –8, dan c = 1. Selanjutnya kita tentukan selesaian-selesaian dari persamaan kuadrat tersebut dengan rumus kuadrat.

Selanjutnya kita uji salah satu selesaiannya, yaitu x = 1 + √3/2 ke dalam persamaan.

Setelah kita uji, ternyata selesaian tersebut memenuhi persamaan kuadrat tersebut. Semoga bermanfaat Pada pembahasan ini kita akan menentukan suatu rumus yang dapat digunakan untuk menentukan selesaian dari persamaan kuadrat ax2 + bx + c = 0. Sebelum itu, kita akan mencoba untuk menyelesaikan persamaan kuadrat 2x2 + 5x + 3 = 0. Perhatikan langkah-langkah dalam menyelesaikan 2x2 + 5x + 3 = 0 dengan melengkapkan kuadrat berikut.
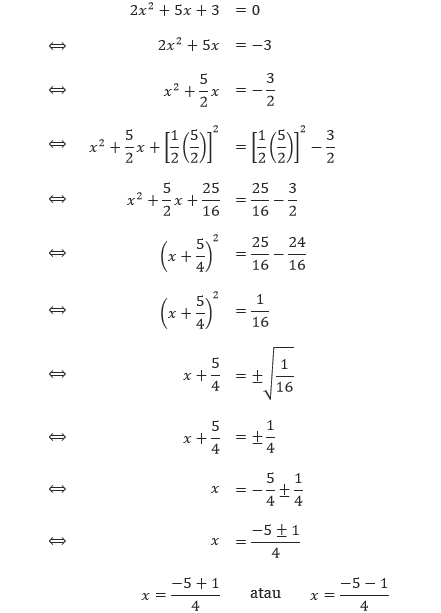
Sehingga diperoleh selesaian-selesaian dari persamaan kuadrat di atas adalah x = –1 dan x = –3/2. Berdasarkan langkah-langkah di atas, kita akan menentukan suatu rumus yang dapat digunakan untuk menyelesaikan persamaan kuadrat ax2 + bx + c = 0.

Solusi-solusi dari persamaan kuadrat ax2 + bx + c = 0 di atas selanjutnya disebut sebagai rumus kuadrat, yang dapat digunakan untuk menyelesaikan semua persamaan kuadrat.
Rumus KuadratCatatan Perlu diketahui bahwa nilai a, b, dan c diperoleh dari persamaan kuadrat yang ditulis ke dalam bentuk standar. Untuk 3x2 – 5x = –7, a = 3, b = –5, tetapi c ≠ –7! Bentuk standar dari persamaan tersebut adalah 3x2 – 5x + 7 = 0, sehingga nilai c dari persamaan tersebut adalah 7.
Jika ax2 + bx + c = 0, dengan a, b, c bilangan real dan a ≠ 0, maka
atau dapat dituliskan menjadi,
Contoh 1: Menyelesaikan Persamaan Kuadrat dengan Rumus Kuadrat
Selesaikan persamaan 4x2 + 1 = 8x dengan menggunakan rumus kuadrat. Nyatakan solusi-solusinya dalam bentuk eksak dan bentuk desimalnya (tiga angka di belakang koma). Ujilah salah satu selesaian eksaknya ke dalam persamaan.
Pembahasan Persamaan kuadrat 4x2 + 1 = 8x memiliki bentuk standar 4x2 – 8x + 1 = 0. Sehingga dari bentuk standar tersebut kita peroleh a = 4, b = –8, dan c = 1. Selanjutnya kita tentukan selesaian-selesaian dari persamaan kuadrat tersebut dengan rumus kuadrat.

Selanjutnya kita uji salah satu selesaiannya, yaitu x = 1 + √3/2 ke dalam persamaan.

Setelah kita uji, ternyata selesaian tersebut memenuhi persamaan kuadrat tersebut. Semoga bermanfaat
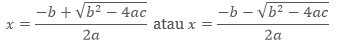
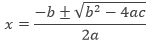
Tidak ada komentar:
Posting Komentar